한다 공부
[딥러닝 입문] 3장 : 선형 회귀, 경사 하강법 (+1장) 본문
3장에 대해 이야기를 하기 전에
머신러닝과, 인공지능에 관련된 용어를 정리해보자
[머신러닝]
우선 기계학습 (=머신러닝은) 학습 방식에 따라 크게
지도학습(supervised learning)
- 회귀(regression), 분류(classification)
비지도학습(unsupervised learning)
- 군집화(clustering), 변환(transform), 연관(association)
강화학습(reinforcement learning)
으로 나누어진다
- 지도학습이란 훈련데이터(입력, 타깃으로 구성)를 사용해 모델(학습을 통해 만들어진 프로그램)을 훈련시키는 것이다.
예를 들면 (입력 => 습도가 nn) 을 통해 (모델로 예측 => 비가 올지, 안올지) 훈련시키는 것이다.
- 비지도학습은 쉽게 말하자면, 데이터의 특성을 파악해 비슷한 것 끼리 그룹핑 하는 것이다.
하지만 앞으로는 지도학습을 중심으로 공부할 예정이다.
- 강화학습은 환경에 최적화된 행동을 수행하고 보상과 현재상태 같은 피드백을 받아 훈련하는 것이다.
[간단한 용어]
우선 1차 선형방정식을 생각해보자
1.5 * x + 0.1 = y 라는 식에서 앞으로 우리가 쓸 용어는
1.5는 가중치, x는 입력, 0.1은 절편, y는 타깃이다.
습도 x를 받아 타깃이 1이 넘으면 비가 온다, 등으로 예측할 수 있다.
[선형 회귀]
선형 회귀는 1차 함수로 표현할 수 있다.
1차 함수 = 기울기와 절편이 주어질 때 만족하는 x y를 찾는것 이라면,
선형 회귀 = x y가 주어질 때 기울기와 절편을 찾는 것 이라고 할 수 있다.
[데이터 준비]
사이킷런이란 파이썬을 대표하는 머신러닝 라이브러리다.
사이킷런에서 데이터 세트를 가져올 수 있다. 당뇨병 환자의 데이터 세트를 가져와보자
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
print(diabetes.data.shape, diabetes.target.shape)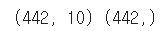
우선 diabetes의 속성 중 data 속성과 target 속성에, 필요한 입력과 타깃 데이터가 넘파이 배열로 저장되어있다.
넘파이 배열의 크기는 shape속성에 저장되어 있으므로, 위와 같이 print한 결과로 입력과 타깃 데이터의 크기가 나온다.
data는 442*10 크기의 2차원 배열,
target은 422개의 요소를 가진 1차원 배열이다.
여기서 행은 샘플이고, 열은 샘플의 특성이다.
여러 특성이 모여 하나의 샘플이 나온다.
입력과 타깃에 저장된 데이터를 출력해보면 해당되는 여러 숫자가 나오는데, 이 숫자는 의사와 같은 전문가들의 영역이므로 우리는 주어진 데이터를 통해 모델만 찾으면 된다.
[데이터 시각화]
위에서 찾은 데이터를 시각화 해보자.
2장에서 쓰인 맷플롯립의 scatter()함수를 통해 산점도로 그릴 것이다.
당뇨병 데이터 세트에는 10개의 특성이 있는데, 모두 표현하면 다차원 그래프가 필요하므로 특성 1개만 사용해서 (세번째 특성) 산점도를 그렸다
from sklearn.datasets import load_diabetes 는 위 코드에서 했다
import matplotlib.pyplot as plt
plt.scatter(diabetes.data[:,2],diabetes.target)
plt.xlabel('x')
plt.ylabel('y')
plt.show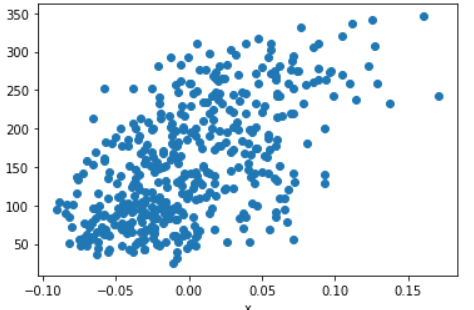
[경사 하강법]
다음 산점도에 가장 가까운 값을 가진 직선을 찾아야한다.
기울기와 절편을 변화해가며 모델(직선)을 조금씩 조정하며 최적화 시키는 알고리즘이 경사 하강법이다.
ŷ 이 기호는 모자쓴 y, 즉 y hat이다.
y= ax+b에서 기울기 a는 w로 표현할 것이고 우리가 예측한 값 y는 ŷ으로 표현할 것이다.
ŷ=wx+b의 형태가 된다.
우리가 찾아야하는 것은 w와 b이다.
[w 찾는 방법]
1. 무작위로 w와 b를 정한다
- 우리의 교재에서는 각각의 값을 1로 잡았다
2. x 샘플 하나를 사용해 ŷ를 구한다
- ŷ을 y_hat변수에 저장한다. 그리고 y_hat=x[0]*w+b로 ŷ을 구한다.
3. ŷ과, 우리가 샘플의 진짜 y을 비교한다
4. ŷ와 y가 가까워질 수 있도록 w와 b를 조정한다
- w값을 조정해보자. ŷ이 y[0]에 가까워져야한다.
5. 반복한다.
.
.
.
4번에서 w를 0.1정도 증가시켜보자.
그리고 얼마나 증가했는지 비교해보면 (ŷ이 증가한 양 나누기 w가 증가한 양) 놀랍게도 우리가 사용한 훈련데이터 x[0]라는 것을 알 수 있다.
[b 찾는 방법]
b의 변화율을 구하면 1이 나온다.
b 변화율 = (ŷ이 증가한 양 나누기 b가 증가한 양) =1
b가 1만큼 증가하면 ŷ도 1만큼 증가한다.
[오차 전역파]
y와 ŷ의 차이가 크게 날 수 있다
이럴 때 w와 b의 값만 바꿔서 계산하기엔 한계가 있다.
y-ŷ 를 이용해서 값을 변경해보자!
이를 오차 전역파 라고 한다.
.
.
.
1. w를 갱신할 때 (y-ŷ)의 값을 (w의 변화율)에 곱하고, w에 더하겠다
w = w + w 변화율 * (y-ŷ)
근데 우리는 w의 변화율이 훈련데이터, 즉 샘플값임을 알았기 때문에, x[1] 샘플에 대해
w_new = w_new + x[1] * (y-ŷ) 임을 유추할 수 있다.
.
.
.
2. b도 마찬가지로 (y-ŷ)의 값을 (b의 변화율)에 곱하고, b에 더하면 된다
우리는 위에서 한 계산을 통해 b의 변화율이 1임을 안다.
b = b + 1(=b의 변화율) * (y-ŷ) 이다.
[에포크]
경사 하강법에서는 주어진 훈련 데이터로 학습을 여러 번 반복한다.
이렇게 전체 훈련 데이터를 모두 이용해서 작업하는 것을 에포크(epoch)라고 한다.
n번의 에포크를 반복하다보면 직선은 전체 데이터의 경향을 잘 따라가게 된다.
[손실 함수]
우선 제곱 오차라는 것에 대해 이야기해보자.
제곱 오차는 오차를 제곱한 것이다. 즉 (y-ŷ)의 제곱이다.
제곱 오차의 기울기를 구하기 위해 가중치에 대해 미분하면 2*(y-ŷ)*(-ŷ)' 이고, ŷ는 w*x+b 이므로 ŷ을 가중치 w에 대해 미분하면 x이다.
즉 -2*(y-ŷ)*x인데, 손실 함수는 상수 곱을 해도 가중치나 절편에 영향을 주지 않으므로 공식을 2로 나눈 -(y-ŷ)*x 을 사용한다
그리고 가중치에서 제곱 오차의 기울기(변화율)을 빼주면 w = w + (y-ŷ)*x 가 된다
절편에 대해서도 제곱 오차를 미분해서 빼주면 b = b + (y-ŷ)가 된다...
이는 위에서 오차 전역파를 이용해 구한 w와 b의 식과 똑같다!!
우와우와우!!
- 손실 함수에 대해 일일이 변화율의 값을 계산하는 것 대신, 편미분을 이용하여 변화율을 계산하는 것이 편하다
그리고 이 변화율을 그레디언트(=그레이디언트, gradient) 라고 부른다
참고로 손실 함수는 비용함수, 목적 함수라고 부른다고 한다.
[파이썬으로 구현]
class Neuron: #뉴런(=유닛) 클래스를 통해 신경망 구현
def __init__(self): #가중치, 절편 초기화
self.w=1.0
self.b=1.0
def forpass(self, x): # 직선 방정식 계산
y_hat=x*self.w+self.b
return y_hat
def backprop(self, x, err):
w_grad = x * err #가중치에 대한 그레디언트 계산
b_grad = 1 * err #가중치에 대한 그레이언트 계산
return w_grad, b_grad
def fit(self, x, y, epochs=100):
for i in range(epochs): #에포크만큼 반복
for x_i, y_i in zip(x, y): #모든 샘플에 대해 반복
y_hat=self.forpass(x_i) # 정방향 계산
err=-(y_i)-y_hat # 오차 계산
w_grad, b_grad = self.backprop(x_i,err) # 역방향 계산
self.w-=w_grad # 가중치 업데이트
self.b-=b_grad #절편 업데이트
# 직선그래프 그리기
plt.scatter(x,y)
pt1=(-0.1, -0.1 * neuron.w + neuron.b)
pt2=(0.15, 0.15 * neuron.w + neuron.b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()
[참고자료] Do it! 딥러닝 입문
'CS > AI' 카테고리의 다른 글
| [AI] YOLOv3를 이용한 Object detection (with Colab) (18) | 2021.11.25 |
|---|---|
| [딥러닝 입문] 4장 : 이진 분류 - 로지스틱 회귀 (0) | 2021.09.26 |
| [딥러닝 입문] 2장 : numpy, matplotlib (0) | 2021.09.19 |


