한다 공부
[C] 우선순위 큐 : 히프정렬 (heap) 본문
우선순위 큐란, 우선순위의 개념을 큐에 도입한 자료구조이다.
선입선출 FIFO(First In First Out)인 큐와 달리
우선순위 큐는 우선순위가 높은 데이터가 먼저 나온다.
우선순위 큐는 배열, 연결리스트를 이용할 수도 있지만
히프라는 자료구조로 구현하려고 한다.
Heap heap heap
히프는 우선순위 큐를 위해 만들어진 자료구조이다
배열로 구현한 히프는 삭제시 O(n)의 복잡도를 가지고
연결리스트 히프는 삭제시 O(n)의 복잡도를 가진다
하지만 히프의 경우 어느정도 정렬이 된 상태기 때문에
O(log n)의 복잡도를 가진다
데이터가 많아질수록 n과 log n의 경우 차이가 크기 때문에
히프를 사용하는 것이 효율성이 높다
히프는 부모 노드의 키 값이, 자식 노드의 키 값보다 항상 큰 이진트리이다.
이러한 히프를 최대 히프(max heap)라고 한다.
=root가 최댓값이 된다
반대로 최소 히프라는 것도 있는데, (min heap)
이 경우에는 부모 노드의 키 값이, 자식 노드의 키 값보다 항상 작다
=root가 최솟값
우리가 구현할 히프는 최대 히프이다.
또한 히프는 완전 이진 트리이다.
이진 탐색 트리와 달리 히프 트리는 중복된 값을 허용한다.
[히프의 삽입]
- 완전 이진 트리의 가장 마지막 위치에 새로운 요소가 삽입된다.
- 부모 노드와 비교하여 삽입 노드가 더 크면 교환한다
- (삽입노드가 부모노드보다 작을 때 까지) 반복
3 5 1 7 이 삽입되었다고 하자
(1) 3이 루트노드로 들어온다
(2) 새로 삽입된 노드 5가 3보다 크므로 5를 루트로 한다.
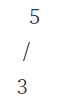
(3) 새로 삽입된 노드 1은 루트인 5보다 작으니 마지막에 삽입
(4) 새로 삽입된 노드 7은 부모노드인 3보다 크니까 교환한다.
7은 그 위의 부모노드이자 루트인 5보다 크므로 루트와 교환한다.
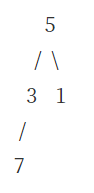
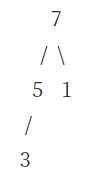
[히프의 삭제]
우리가 구현할 최대 히프의 경우,
최댓값을 가진 요소를 삭제하는 것인데
최댓값은 루트에 존재한다.
그러므로 루트 노드를 삭제해보자
- 루트 노드를 삭제하고, 그 자리에 히프의 마지막 노드를 가져온다
- 새로 변경된 루트 값을 자식노드와 비교해보면서 자식노드가 더 크면 교환을 한다
- (자식노드가 루트노드보다 작을 때 까지) 반복
구현을 해보자!
위의 트리 값을 히프에 넣었다
#include<stdio.h>
#include<stdlib.h>
#define MAX_ELEMENT 20
typedef struct {
int key; //값
}element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size; //heap안 저장된 요소의 개수
}HeapType;
HeapType* create() {
return (HeapType*)malloc(sizeof(HeapType));
}
void init(HeapType* h) {
h->heap_size = 0;
}
void insert_max_heap(HeapType* h, element item) {
int i;
//처음 넣는거라면 i가 1이 된다
i = ++(h->heap_size);
//새로 넣으려는 노드의 부모노드 찾기!
//부모노드보다 내가 작거나 && 내가 root가 될 때까지 반복
while ((item.key > h->heap[i / 2].key) && (i != 1)) {
//내가 더 크면, 부모노드자리에 내가 올라감
h->heap[i] = h->heap[i / 2];
// while 한번 더 돌면 원래 부모였던 노드의, 부모노드 값 ->
//즉 (=할아버지 할머니 노드^^) 랑 나랑 비교하게 되는 것
i = i / 2;
}
h->heap[i] = item;
}
element delete_max_heap(HeapType* h) {
element item, temp;
item = h->heap[1];
temp = h->heap[h->heap_size];
//h->heap[h->heap_size]은 힙 배열의 마지막 값
h->heap_size = h->heap_size - 1;
int parent, child;
parent = 1;
child = 2;
while (child <= h->heap_size) {
//현재 노드의 자식노드 중 더 큰 자식노드 찾기
//(왼/오 자식 중 더 큰거 찾기)
if ((child < h->heap_size) && (h->heap[child].key < h->heap[child + 1].key))
child++; //오른쪽 자식 노드의 값이 더 큼
//마지막 값인 temp가 루트로 올라가서
//자식노드들과 비교 하면서, 자식보다 작으면 내려가는 상황
//자식노드보다 크면 교환 멈추기
if (temp.key >= h->heap[child].key)
break;
//자식노드보다 작으면
//한 단계 아래로 이동하며 교환
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}
int main() {
element e1 = { 3 }, e2 = { 5 }, e3 = { 1 }, e4 = { 7 }, e5 = { 4 };
element a1;
HeapType* heap;
heap = create();
init(heap);
insert_max_heap(heap, e1);
insert_max_heap(heap, e2);
insert_max_heap(heap, e3);
insert_max_heap(heap, e4);
insert_max_heap(heap, e5);
for (int k = 1; k <= heap->heap_size; k++)
printf("%d ", heap->heap[k]);
a1 = delete_max_heap(heap);
printf("\n\nmax값 인출 %d\n\n", a1.key);
for (int k = 1; k <= heap->heap_size; k++)
printf("%d ", heap->heap[k]);
free(heap);
}

히프 정렬
데이터들을 히프에 넣는다.
그리고 히프에서 하나씩 꺼내서 배열의 끝쪽부터 저장하고
처음부터 출력하면 정렬이 된다.
n개의 요소들은 O(n*log n)시간 안에 정렬된다.
#include<stdio.h>
#include<stdlib.h>
#define MAX_ELEMENT 20
//heap 구현 코드와 동일 한 부분, 시작
typedef struct {
int key;
}element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
}HeapType;
HeapType* create() {
return (HeapType*)malloc(sizeof(HeapType));
}
void init(HeapType* h) {
h->heap_size = 0;
}
void insert_max_heap(HeapType* h, element item) {
int i;
i = ++(h->heap_size);
while ((item.key > h->heap[i / 2].key) && (i != 1)) {
h->heap[i] = h->heap[i / 2];
i = i / 2;
}
h->heap[i] = item;
}
element delete_max_heap(HeapType* h) {
element item, temp;
item = h->heap[1];
temp = h->heap[h->heap_size];
h->heap_size = h->heap_size - 1;
int parent, child;
parent = 1;
child = 2;
while (child <= h->heap_size) {
if ((child < h->heap_size) && (h->heap[child].key < h->heap[child + 1].key))
child++;
if (temp.key >= h->heap[child].key)
break;
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}
//heap 구현 코드와 동일 한 부분, 끝
//heap 정렬 코드
void heap_sort(element a[], int n) {
int i;
HeapType* h;
h = create();
init(h);
//값을 히프에 넣고
for (int i = 0; i < n; i++)
insert_max_heap(h, a[i]);
//최댓값부터 배열 뒤쪽에 넣는다
for (i = n - 1; i >= 0; i--) {
a[i] = delete_max_heap(h);
}
free(h);
}
int main() {
element list[5] = { 3, 5, 1, 7, 4 };
heap_sort(list, 5);
for (int i = 0; i < 5; i++)
printf("%3d", list[i].key);
}
허프만 코드 (Huffman codes)
허프만 코드는 메세지의 내용을 압축하는 데에 쓰이는 가변 길이 코드이다.
빈도수에 따라 빈도수가 많으면 글자의 비트를 적게 할당하고
빈도수가 적으면 조금 큰 크기의 비트수를 할당한다.
a가 100번 나오고 e가 10번 나오는 메세지가 있다고 하자.
아스키 코드의 경우 한 글자가 3비트이기 때문에
3*110=330, 330비트가 쓰인다.
하지만 허프만 코드를 이용해서 a에 2비트, e에 3비트를 할당하면
2*100+3*10=230,
아스키 코드 보다 무려 100비트나 압축할 수 있다.
이러한 허프만 코드를 생성하는 데에 히프가 쓰인다.
허프만 코드 생성과정에 대해 간략하게 알아보자.
이는 히프로 구현할 수도 있다.
글자(빈도수)가 다음과 같이 주어졌다고 하자
s(4), i(6), n(8), t(12), e(15)
우선 가장 작은 두 값을 고른다. 4와 6 !
그리고 4와 6을 합쳐서 새 값을 만든다.
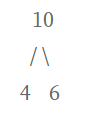
그러면 새 값인 10과, 남은 빈도 값인 8, 12, 15 !
총 4개의 값이 남는다.
그럼 이 4개의 값 중 가장 작은 값 2개를 고른다. 8과 10 !
이 8과 10을 이용해 새 값을 만든다.
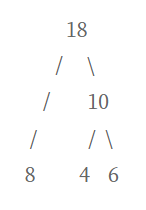
그러면 새 값인 18과, 남은 빈도 값인 12, 15가 남는다.
12 15 18 중 가장 작은 값인 12와 15를 합친다.
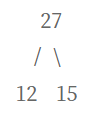
그러면 현재 값은 18과 27이 남았다. 이 둘을 합치자
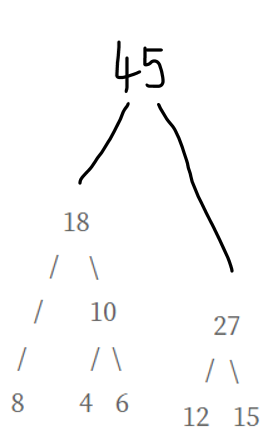
이렇게 된다
그럼
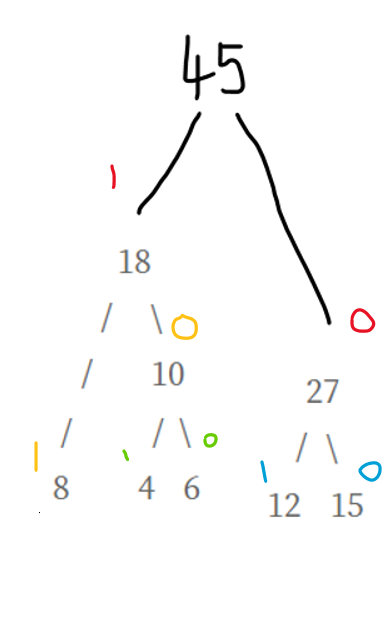
라벨 값을 붙여준다.
여기서는 왼쪽 자식노드에1,
오른쪽 자식노드에 0을 붙였다. (색 있는 글씨)
그리고 간선을 따라 라벨 값을 읽어주면 된다.
s(4) -> 빈도수 4, 알파벳 s인 글자는 코드가 101,
i(6)는 100,
n(8)은 11,
t(12)는 01,
e(15)는 00이 된다.
see 의 경우 허프만 코드로 변경시키면 1010000이 된다.
허프만 코드의 경우 한 단어가 두 가지 방법으로 읽히는 경우는 없다.
01000011의 경우 해독하면
앞부분이 0으로 시작하는건 00 또는 01인데 0100... 이므로 01, 즉 t이다
01을 제외하면 000011인데 같은 방법으로 00 00 11로 해독할 수 있다.
그러면 e e n 이고 01000011의 경우 teen이 된다
net의 경우는 110001로 코드화할 수 있다.
.
.
.
우선순위 큐와 히프 완료!
후반부도 열공하자,,
2년만에 다시 보는거라
기억이 새록새록하다..
약간 초면..
복습말고도 관련된 백준 문제 풀어야하는데 언제풀지 ㅠㅠ!!
[참고자료] C언어로 쉽게 풀어 쓴 자료구조, 생능출판, 천인국 공용해 하상호 지음
'Algorithm > 정리' 카테고리의 다른 글
| [C++] 에라토스테네스의 체 (0) | 2022.02.26 |
|---|---|
| [C++] 유클리드 호제법 (0) | 2022.02.26 |
| [C] 트리 : 이진 탐색 트리 (0) | 2021.08.18 |
| [C] 트리 : 이진트리의 연산 (0) | 2021.08.17 |
| [C] 트리 : 이진트리의 전위, 중위, 후위, 레벨 순회 (0) | 2021.08.17 |


