한다 공부
[C] 트리 : 이진트리의 전위, 중위, 후위, 레벨 순회 본문
아까 이진트리를 구현할 때
10
/ \
20 30
위와 같은 트리를 어떻게 순회해야 잘 순회했다고 소문이 날까?
여기엔 크게 3가지 순회가 있다.
전위 순회란
루트를 방문하고 왼쪽 서브트리, 오른쪽 서브트리를 방문하는 순회이다.
위의 트리를 예시로 들면 10 -> 20 -> 30 순으로 순회하는 것이다.
아래 코드에서 preorder이라는 함수를 통해 구현을 할 것이다.
중위 순회란
왼쪽 서브트리 -> 루트 -> 오른쪽 서브트리 순으로 방문하는 순회이다.
위 트리를 예시로 들면 20 -> 10 -> 30 순으로 순회한다.
아래 코드에서 inorder이라는 함수를 통해 구현을 할 것이다.
후위 순회란
왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 순으로 방문하는 순회이다.
위 트리에서 20 -> 30 -> 10 으로 순회하는 것이다.
postorder이라는 함수를 통해 구현을 해보자!
교재 p.276 Quiz의 트리를 구현하고 순회해보자
17
/ \
15 93
/ / \
5 35 95
/
22
트리가 혹시 업로드 중에 깨질까봐.. 사진도 첨부!
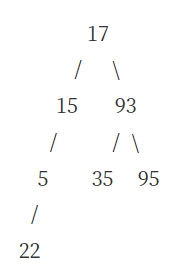
전위 순회의 결과 17 15 5 93 35 22 95
중위 순회의 결과 5 15 17 22 35 93 95
후위 순회의 결과 5 15 22 35 95 93 17
..이 나와야 한다.
노드의 순서는 아래와 같다.
n1
/ \
n2 n3
/ / \
n4 n5 n6
/
n7
#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode {
struct TreeNode* left;
int data;
struct TreeNode* right;
}TreeNode;
TreeNode n7 = { NULL,22,NULL };
TreeNode n6 = { NULL,95,NULL };
TreeNode n5 = { &n7,35,NULL };
TreeNode n4 = { NULL,5,NULL };
TreeNode n3 = { &n5,93,&n6 };
TreeNode n2 = { &n4,15,NULL };
TreeNode n1 = { &n2,17,&n3 };
TreeNode* root = &n1;
//전위 순회 = 루트, 왼, 오
void preorder(TreeNode* root) {
if (root != NULL) {
printf("[%d] ", root->data); //루트 방문
preorder(root->left); //순환 - 재귀함수, 왼쪽 노드를 루트로 전달해서 다시 전위 순회
preorder(root->right); //왼쪽 서브트리 모두 방문 후 오른쪽 서브트리 방문
}
}
//중위 순회 = 왼, 루트, 오
void inorder(TreeNode* root) {
if (root != NULL) {
inorder(root->left); //왼쪽 서브트리부터 방문
printf("[%d] ", root->data); //루트 방문
inorder(root->right); //오른쪽 서브트리 방문
}
}
//후위 순회 = 왼, 오, 루트
void postorder(TreeNode* root) {
if (root != NULL) {
postorder(root->left); //왼쪽 서브트리부터 방문
postorder(root->right); //오른쪽 서브트리 방문
printf("[%d] ", root->data); //마지막에 루트 방문
}
}
int main() {
printf("전위 순회 : ");
preorder(root);
printf("\n중위 순회 : ");
inorder(root);
printf("\n후위 순회 : ");
postorder(root);
}여담으로,
TreeNode n1부터 선언하면 에러가 난다.
전역변수를 정의할 때, n1의 링크에 n2 n3를 달아야하는데
n2 n3가 정의되지 않은 상태이기 때문이다.
그러므로 단말노드인 n7부터 선언했다.
출력 결과..!
두근 두근

그렇다면 레벨 순회란 무엇일까?
레벨 순회는 레벨 순서대로 순회하는 방법이다.
1레벨의 n1을 순회하고
2레벨의 n2 n3를 차례로 순회하고,
3레벨의 n4 n5 n6,
4레벨의 n7을 순회하는 것이 레벨 순회이다.
레벨 순회를 하기 위해서는 큐를 사용한다.
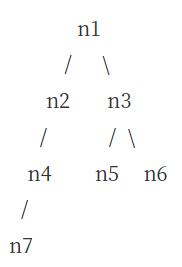
순서
(레벨1)
우선 큐에 n1을 넣는다.
n1을 꺼내며 (= n1을 방문)
n1의 자식인 n2와 n3를 큐에 넣는다.
(레벨2) 현재 큐 : n2 n3
큐의 첫 번째에 있는 n2를 꺼내며 방문한 후,
n2의 자식인 n4를 넣는다.
그러면 큐에는 n3 n4가 들어있게 된다.
n3를 꺼내며 방문하며 n3의 자식인 n5와 n6를 큐에 넣는다.
(레벨3) 현재 큐 : n4 n5 n6
n4를 꺼내며 방문하면서
n4의 자식인 n7을 큐에 넣는다. (레벨4)
큐에는 n5 n6 n7이 있게 된다.
큐에 남은 것들을 순서대로 꺼내면 레벨 순회가 끝난다.

아까와 같은 트리를 레벨 순회 해보면
17 15 93 5 35 95 22 가 나올 것이다.
구현을 해보자!
#include<stdio.h>
#include<stdlib.h>
typedef struct TreeNode {
struct TreeNode* left;
int data;
struct TreeNode* right;
}TreeNode;
//원형 큐 코드
#define MAX_QUEUE_SIZE 100
typedef TreeNode* element;
typedef struct {
int front;
int rear;
element data[MAX_QUEUE_SIZE];
}QueueType;
//큐 초기화 함수
void init_queue(QueueType* q) {
q->front = q->rear = 0;
}
//오류 함수
void error(const char* message) {
fprintf(stderr, "%s\n", message);
exit(1);
}
//overflow check
int is_full(QueueType* q) {
if ((q->rear + 1) % MAX_QUEUE_SIZE == q->front) return 1;
else return 0;
}
//underflow check
int is_empty(QueueType* q) {
if (q->front == q->rear) return 1;
else return 0;
}
//삽입
void enqueue(QueueType* q, element item) {
if (is_full(q)) {
error("queue overflow");
return;
}
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
//삭제
element dequeue(QueueType* q) {
if (is_empty(q)) {
error("queue underflow\n");
return -1;
}
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}
//레벨 순회
void level_order(TreeNode* root) {
QueueType q;
init_queue(&q);
if (root == NULL) return;
enqueue(&q, root);
while (!is_empty(&q)) {
root = dequeue(&q);
printf("[%d] ", root->data);
if (root->left) enqueue(&q, root->left);
if (root->right) enqueue(&q, root->right);
}
}
TreeNode n7 = { NULL,22,NULL };
TreeNode n6 = { NULL,95,NULL };
TreeNode n5 = { &n7,35,NULL };
TreeNode n4 = { NULL,5,NULL };
TreeNode n3 = { &n5,93,&n6 };
TreeNode n2 = { &n4,15,NULL };
TreeNode n1 = { &n2,17,&n3 };
TreeNode* root = &n1;
int main() {
printf("레벨 순회 : ");
level_order(root);
printf("\n");
}

트리 순회 4가지 방법을 알아보았다.
다음 포스팅에서는 트리의 다양한 연산들에 대해 알아 볼 예정이다.
이번주도 파이팅!!
[참고자료] C언어로 쉽게 풀어 쓴 자료구조, 생능출판, 천인국 공용해 하상호 지음
'Algorithm > 정리' 카테고리의 다른 글
| [C] 트리 : 이진 탐색 트리 (0) | 2021.08.18 |
|---|---|
| [C] 트리 : 이진트리의 연산 (0) | 2021.08.17 |
| [C] 트리 : 이진트리 (0) | 2021.08.16 |
| [C] 연결리스트 : 스택, 큐 (0) | 2021.08.15 |
| [C] 연결리스트 : 원형, 이중연결리스트 (0) | 2021.08.15 |



